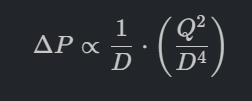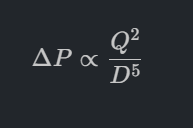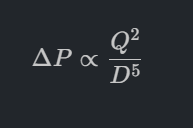
กฎกำลัง 5 ของขนาดท่อ (Diameter order no.5) ส่งผลกระทบอย่างรุนแรงและโดยตรงต่อ การเลือกขนาดของปั๊ม (Pump Selection) และ ต้นทุนพลังงาน ในการดำเนินงาน (OPEX) โดยมีรายละเอียดดังนี้
ผลต่อขนาดแรงดัน (Pump Head) ที่ต้องเลือกใช้
กฎนี้ระบุว่าค่าความดันลดเนื่องจากแรงเสียดทาน (Friction Loss) จะเพิ่มขึ้นเป็นกำลัง 5 เมื่อขนาดเส้นผ่านศูนย์กลางท่อลดลง (ที่อัตราการไหลคงที่)
ผลกระทบ: หากเลือกขนาดท่อเล็กลงเพียงนิดเดียว ปั๊มที่เลือกจะต้องมี Total Dynamic Head (TDH) หรือแรงดันด้านขาออกที่สูงขึ้นอย่างมหาศาลเพื่อเอาชนะแรงเสียดทานในท่อที่เพิ่มขึ้นนั้น เพื่อให้ได้อัตราการไหลเท่าเดิม
ตัวอย่าง: การลดขนาดท่อลงครึ่งหนึ่ง จะทำให้ปั๊มต้องทำแรงดันเพิ่มขึ้นถึง 2^5 หรือ 32 เท่า
ผลต่อกำลังงานและขนาดมอเตอร์ (Power Requirement)
กำลังงานที่ปั๊มต้องใช้ (Pump Power) แปรผันตรงกับผลคูณของ อัตราการไหล (Q) และ แรงดัน (Head)
ความสัมพันธ์: ในเมื่อแรงดัน (Pressure Drop) แปรผกผันกับขนาดท่อยกกำลัง 5 (1/D^5) ดังนั้น พลังงานที่ปั๊มต้องใช้ก็จะแปรผกผันกับขนาดท่อยกกำลัง 5 เช่นกัน
ผลกระทบ: การเลือกท่อขนาดเล็กจะทำให้ต้องเลือกปั๊มที่มีขนาดมอเตอร์ใหญ่ขึ้นมาก และส่งผลให้ค่าไฟฟ้าตลอดอายุการใช้งาน (Operating Cost) สูงขึ้นมาก
ทำไมถึงเป็นกำลัง 5
สาเหตุที่ค่าความดันลด (Pressure Drop) ในท่อแปรผกผันกับขนาดเส้นผ่านศูนย์กลางท่อยกกำลัง 5 เกิดจากการเปลี่ยนตัวแปรในการคำนวณจาก “ความเร็ว” (V) มาเป็น “อัตราการไหลเชิงปริมาตร” (Q)
สามารถอธิบายที่มาทางคณิตศาสตร์ได้เป็นขั้นๆ ดังนี้:

เริ่มจากสูตรพื้นฐาน Darcy-Weisbach: สูตรมาตรฐานในการหาค่าความดันลด (ΔP) จะขึ้นอยู่กับความเร็วยกกำลังสอง และแปรผกผันกับขนาดท่อกำลังหนึ่ง:
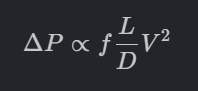
โดยที่ L = ความยาว, D = เส้นผ่านศูนย์กลาง, V = ความเร็ว
ความสัมพันธ์ระหว่าง ความเร็ว (V) และ อัตราการไหล (Q): ในทางปฏิบัติ วิศวกรมักรู้อัตราการไหล (Q) มากกว่าความเร็ว (V) ซึ่งความสัมพันธ์คือ:
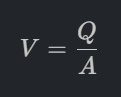
และเนื่องจากพื้นที่หน้าตัดของท่อกลม (A) คำนวณจาก πD^2/4 ทำให้เราได้ความสัมพันธ์ว่า:
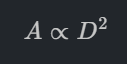
ดังนั้น ความเร็วจะสัมพันธ์กับขนาดท่อดังนี้:
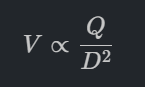
นำ V (ซึ่งเท่ากับ Q/D^2) ไปยกกำลังสองเพื่อเตรียมเข้าสูตร Darcy จะได้:
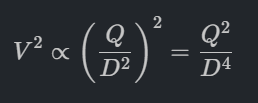
แล้วนำค่าที่ได้ไปเข้าสูตร Darcy-Weisbach