SIL verification by Markov Model Method

แสดงความเห็นโดยpongsakorn monturatเขียนแล้วในSIL

บทความนี้จะนำเสนอและอธิบายถึง Markov Model ซึ่งเป็นเทคนิคการสร้างแบบจำลองทางคณิตศาสตร์ที่ให้ค่าที่แม่นยำสูง เพื่อใช้ในการคำนวณค่าความน่าจะเป็นของการล้มเหลวเมื่อมีความต้องการ (Probability of Failure on Demand หรือ PFD) และสนับสนุนกระบวนการทวนสอบระดับความสมบูรณ์ด้านความปลอดภัย (SIL Verification) ได้อย่างน่าเชื่อถือ

Probability of Failure on Demand (PFD) คืออะไร

ก่อนที่จะเจาะลึกถึง Markov Model สิ่งสำคัญคือต้องทำความเข้าใจหน่วยวัดพื้นฐานที่ใช้ประเมินประสิทธิภาพของระบบความปลอดภัย นั่นคือ ความน่าจะเป็นของการล้มเหลวเมื่อมีความต้องการ (Probability of Failure on Demand หรือ PFD) ซึ่งถือเป็นรากฐานที่สำคัญที่สุดของการจำแนกระดับความสมบูรณ์ด้านความปลอดภัย หรือ SIL (Safety Integrity Level)

โดย Probability of Failure on Demand (PFD) คือค่าความน่าจะเป็นที่ฟังก์ชันด้านความปลอดภัย (Safety Instrumented Function – SIF) จะล้มเหลวและไม่สามารถทำงานตามที่ออกแบบไว้ได้เมื่อเกิดสภาวะที่ต้องการการทำงานของระบบ (Demand) โดยค่า PFD นี้จะบ่งชี้ถึงประสิทธิภาพที่จำเป็นของ SIF เพื่อให้บรรลุค่า Risk Reduction Factor (RRF) หรือปัจจัยการลดความเสี่ยงที่ต้องการ ทำให้ PFD ไม่ใช่เป็นเพียงค่าความน่าจะเป็นเชิงนามธรรม แต่เป็นเป้าหมายด้านประสิทธิภาพที่จับต้องได้และผูกโยงกับการลดความเสี่ยงโดยตรง

สำหรับวัตถุประสงค์ของการทวนสอบค่า SIL (SIL Verification) ค่าที่นำมาใช้โดยเฉพาะคือ ค่าเฉลี่ยความน่าจะเป็นของการล้มเหลวเมื่อมีความต้องการ (Average Probability of Failure on Demand หรือ PFDavg) ซึ่งแสดงถึงค่าเฉลี่ยความไม่พร้อมใช้งาน (Unavailability) ของฟังก์ชันความปลอดภัยตลอดช่วงระยะเวลาการทดสอบ (Proof-Test Interval)

ทำความรู้จัก Markov Model

Markov Model คือแบบจำลองทางคณิตศาสตร์ที่อิงตามสถานะ (State-Based) ซึ่งใช้วิเคราะห์การเปลี่ยนแปลงของระบบระหว่างสถานะการทำงานต่างๆ เมื่อเวลาผ่านไป โดยมีลักษณะเด่นที่สำคัญดังนี้

  • การวิเคราะห์ตามสถานะ (State-Based Analysis): แบบจำลองจะพิจารณาระบบในสถานะต่างๆ ที่ชัดเจน เช่น OK (ทำงานปกติ), Degraded (ระบบทำงานได้แต่มีส่วนประกอบล้มเหลว โดยอาศัยระบบสำรอง ซึ่งสามารถแบ่งย่อยเป็นสถานะที่สำคัญ เช่น Degraded – Fail Detected และ Degraded – Fail Undetected), Fail-Safe (ล้มเหลวในรูปแบบที่ปลอดภัย), และ Fail-Dangerous (ล้มเหลวในรูปแบบที่เป็นอันตราย)
  • การสร้างแบบจำลองการเปลี่ยนผ่าน (Modeling Transitions): ใช้ “อัตราการเปลี่ยนผ่าน” (Transition Rates) ซึ่งคำนวณจากอัตราการล้มเหลวของอุปกรณ์ หรือ Failure Rate (λ) และอัตราการซ่อมบำรุง หรือ Restore Rate (μ) เพื่อหาค่าความน่าจะเป็นในการที่ระบบจะย้ายจากสถานะหนึ่งไปยังอีกสถานะหนึ่ง
การเปลี่ยนสถานะจาก OK ไปเป็น Fail โดยผ่านอัตราการล้มเหลวของอุปกรณ์ Failure Rate
มีทั้งการเปลี่ยนสถานะจาก OK ไปเป็น Fail และการแก้ไขจาก Fail กลับมาเป็น OK โดยผ่านอัตราการซ่อมบำรุง หรือ Restore Rate
  • คำนวณความน่าจะเป็นของสถานะ: แบบจำลอง Markov Model จะใช้ Transition Matrix ซึ่งแสดงถึงความน่าจะเป็นในหนึ่งขั้นของการเปลี่ยนผ่านระหว่างสองสถานะใดๆ เพื่อแก้สมการทางคณิตศาสตร์และหาค่าความน่าจะเป็นที่ระบบจะอยู่ในสถานะล้มเหลวที่เป็นอันตราย (Probability of Failure on Demand) ในช่วงเวลาการทดสอบ (Proof Test Interval) ที่กำหนด ผลลัพธ์ที่ได้นี้คือค่า PFDavg
  • ผลลัพธ์ที่ขึ้นอยู่กับเวลา (Time-Dependent Results): มีความสามารถในการคำนวณความน่าจะเป็นของการอยู่ในสถานะใดๆ ณ เวลาที่กำหนด ซึ่งเป็นสิ่งจำเป็นอย่างยิ่งสำหรับการคำนวณค่า PFDavg

ดังนั้นผลลัพท์ที่ได้จากการศึกษาค่า PFDavg ที่ได้ สามารถนำไปเปรียบเทียบกับข้อกำหนดตามมาตรฐาน (เช่น IEC 61508) เพื่อทวนสอบว่าการออกแบบระบบนั้นบรรลุระดับความสมบูรณ์ด้านความปลอดภัย (Safety Integrity Level หรือ SIL) ที่ต้องการหรือไม่

The benefit of Markov Modeling

ข้อดีที่สำคัญที่สุดของการศึกษา Markov Mode คือ การมีความยืดหยุ่นที่เหนือกว่า (Superior Flexibility) วิธีแบบอื่นๆทำให้สามารถสร้างแบบจำลองสำหรับสถานการณ์ที่ซับซ้อนได้อย่างมีประสิทธิภาพ เช่น

  • สามารถวิเคราะโครงสร้างที่มีความซับซ้อน เช่น 1-out-of-2 or 2-out-of-3 voting systems
  • สามารถวิเคราะห์ระบบที่มีพิจารณาตัวแปรเรื่องการซ่อมบำรุงเข้ามาเพิ่ม คือ Markov model สามารถศึกษาได้ทั้งระบบแบบ Non-Restorable และแบบ Restorable
  • สามารถประยุกต์ใช้กับ รูปแบบความล้มเหลวที่หลากหลาย, และกลยุทธ์การซ่อมบำรุงที่แตกต่างกัน
  • สามารถประยุกต์ใช้ Markov Model กับการคำนวนหาค่าต่างๆ ที่เกี่ยวกับ Reliability Engineering เช่น
    • Steady-state probability โดยใช้ linear equation;
    • Time-dependent probability โดยใช้ differential equation;
    • Discrete-time state probability โดยใช้ matrix multiplication; และ
    • Mean Time To Failure (MTTF) โดยใช้ matrix subtraction และ inversion.

ตัวอย่างการใช้งาน Markov Modeling

ตัวอย่าง#1 ของการเขียนสถานะ หรือ State ของ Transmitter หนึ่งตัว ว่าจะมีสถานะ 4 สถานะ ได้แก่ OK, Fail Safe, Fail Dangerous Detected, และ Fail Dangerous Undetected ตามรูปข้างล่าง

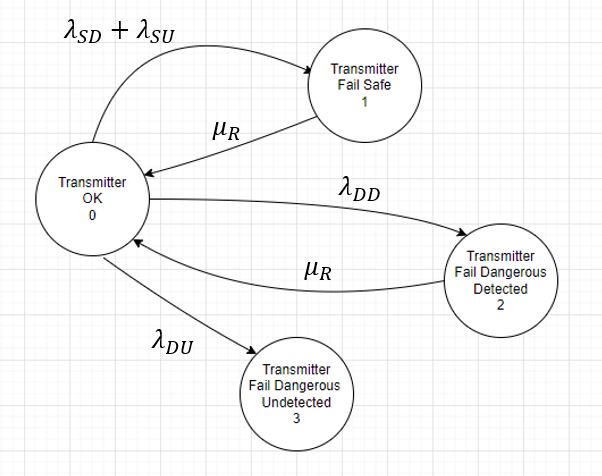
และสามารถนำข้อมูลนี้มาเขียน P-Matrix และมีค่าคำนวนต่างๆ ดังนี้

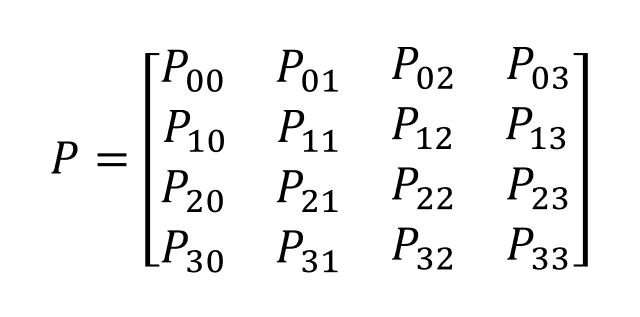
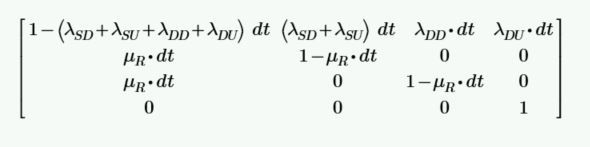
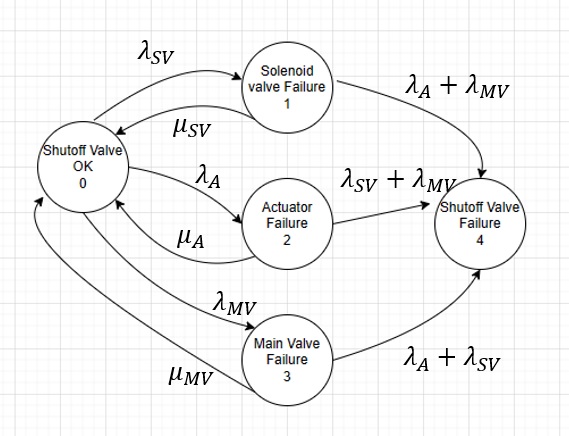
ตัวอย่าง#2 ของการเขียนสถานะของ Shut-off valve ที่มีองค์ประกอบสามส่วน คือ Solenoid Valve, Actuator Valve และ ตัว Main valve โดยการเสียอย่างใดอย่างหนึ่ง (1-out-of-3) ตัว Shut-off valve ก็จะเสีย

The other example is the markov modelling of shutoff valve which typically will compose 3 mains components, main valve, actuator, and solenoid valve.