Blast explosions are typically associated with flammable cloud when it is formed during the leakage of flammable gases. If its direct ignition once released lead to a flash fire. If, however, its ignition is for some delayed (5-10 mins), then a Vapor Cloud Explosion (VCE) is the probable outcome.
The study of blast explosions involves understanding the dynamics, effects, and mitigations of these explosions.
Key aspects of blast explosion studies include:
Shockwave Propagation: Blast explosions generate shockwaves the travel through the air, causing damage to structures and injuring people. Understanding how these shockwaves propagate is crucial for assessing the potential impact of an explosion.
Blast Effects: The study can demonstrate the effects of blast waves on structures, infrastructure, and the human body. This includes the evaluation of overpressure (peak pressure), impulse (the total pressure applied over time), and the duration of the blast.
Structural Response: Buildings and other structures react differently to blast loads depending on their design and construction. The design aims to develop methods to design structures that can better withstand blast impacts.
Human Injury and Protection: Blast explosions can cause injuries to humans, including primary injuries from the blast wave, secondary injuries from flying debris, and tertiary injuries from being thrown or crushed. Studies focus on protective measures and strategies to minimize these injuries.
Two (2) main important parameters output from Blast Explosion Study
- Peak Pressure (Overpressure): The peak pressure, also known as overpressure, refers, to the maximum pressure level reached by the blast wave during its propagation. It is usually measured in (psi) or (Pa). Peak pressure is a critical factor in assessing the potential damage caused by a blast. Higher peak pressures are associated with greater destructive potential.
- Impulse: Impulse is the cumulative effect of the blast wave over time. It is the integral of the pressure-time curve and represents the total momentum imparted by the blast wave. Impluse is calculated by integrating the pressure-time curve over a specified time interval and is expressed in (psi.s) or (N.s/m2)
Damage estimated based on overpressure published by V.J Clancey “Diagnostic Features of Explosion Damage” are given in below table.
| psig | kPa | Damage |
| 0.3 | 2.07 | “Safe distance” probability 0.95 of no serious damage below this value. Projectile limit. Some damages to house ceiling. 10% window glass broken. |
| 2 | 13.8 | Partial collapse of walls and roofs of house |
| 3 | 20.7 | Heavy machines (3,000 lbs) in industrial buildings suffer little damage. Stell frame building distort and pull away from foundation. |
Parameters Significantly Affecting the Behavior of Explosions
- Ambient temperature
- Ambient pressure
- Composition of explosive material
- Physical properties of explosive material (material reactivity)
- Nature of ignition source i.e. type, energy, and duration
- Geometry of surrounding i.e. confined or unconfined space
- Degree of confinement
- Amount of combustible material
- Turbulence of combustible material
- Time before ignition
Deflagration and Detonation
The damage effects from explosion depend highly on whether the explosion results from a detonation or a deflagration. Deflagration and detonation are both processes of rapid combustion, but they differ in terms of the speed of the combustion wave and the mechanisms involved. The below table is a summarize of the difference between deflagration and detonation.
| Deflagration | Detonation | |
| Speed | Subsonic combustion process | Supersonic combustion process |
| Propagation | Combustion wave moves through the substance relatively slowly. | Combustion wave moves through the substance very rapidly. |
| Shock Wave | No strong shock wave produced. | Shock wave is the formation of Detonation. |
| Example | Burning of a piece of paper. | Explosion of dynamite. |
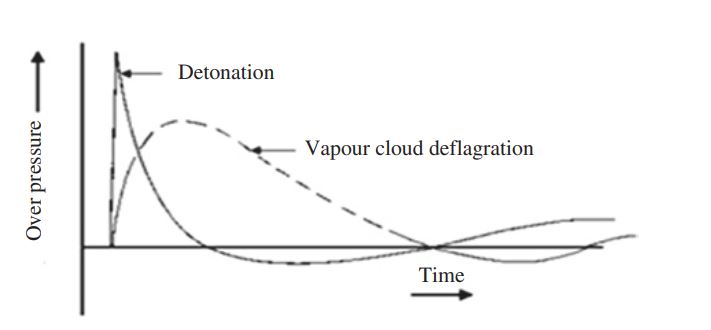
In the detonation mode, the flame front travels as a shock wave and exceeds the velocity of sound (330 m/s) typically of the order of 2,000 – 3,000 m/s. A detonation generates greater pressure than a deflagration explosion flame.
A deflagration can also evolve into a detonation. This is called a deflagration to detonation transition (DDT). The transition is particularly in pipes but unlikely in vessels or open spaces since in the piping system the energy from a deflagration can convert to pressure wave, resulting in an increase in the adiabatic pressure rise.
Key parameters
Ignition of the flammable gas, dust or mist cloud will result in the propagation of a frame front, or deflagration wave. The effect of a deflagration is to increase the pressure-volume product due to a large rise in temperature and a change in mole amount of gas present. Hence, based on this explanation, the relationship of ideal gas equation of state can be applicable.
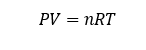
For the explosion to take place, three conditions must be presented.
- Sufficient quantities of flammable fuel, air, and ignition source or cloud dimension;
- Flame speed (Sf); and
- System geometry.
Cloud dimension, R (m), is derive from the volume, V (m3) of the vapor cloud, which is composed from flammable gas and air on the surface. This can be calculated from the reaction’s stoichiometry. The geometry of the cloud dimension could be considered as a hemisphere, as

Burning velocity is defined as the speed at which the flame front propagates through the flammable mixture relative to the unburned mixture ahead of the flame. However, burning velocity does not take into account the flame expansion relative to stationary objects. Hence, when such expansion is taken into account, the term flame speed is used.
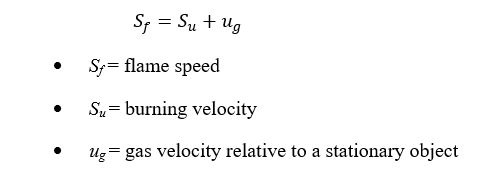
As a minimum of flame speed,

However, flame speed (Sf)can become high, particularly in the tube situation where displacement of the gas ahead of the flame creates pipe flow turbulence. Flame speed without turbulence for hydrogen without stationary objects would be about 24 m/s (laminar) but turbulence could lead to flame speed of 240 m/s or more. Hence, the system geometry is more contribute to the pressure of explosion than the flame speed significantly.
The value of the estimate the burning velocity (Su) for a number of gases in air can be referred to NFPA 68.
System geometry
Open area
If the explosion occurs in the unconfined space, it can be called as unconfined vapor or dust cloud deflagration which can presents the hazards of an expanding fireball rather than the detonation since it does not produce large localized overpressure.
The size of fireball generated can be estimated by assuming that a fixed amount of fuel burns with a stoichiometric equivalent amount of air to yield a burned volume at the flame temperature. The increase in volume in volume of the burned mass is estimated by using the relationship of ideal gas equation of state.

For example, the maximum theoretical hydrocarbon’s pressure, with initial pressure and temperature between 1 and 40 bar and 0-300oC.

Shepherd et al. (1997) developed a relatively simple and sufficient accurate model on the basis of energy conservation law applied to a constant volume adiabatic system.

Partially confined
A partially confined deflagration is represented by combustion of a vapor or dust cloud in a small volume of a larger enclosure which the total pressure rise is proportional to the volume of gas burned. The example case are;
- Explosion inside the building;
- Explosion in vessels and pipes
In case of building with some opening, A simple method to determine the peak pressure has been described by Weibull (1968) as follows.

Unconfined Vapor Cloud Explosion (UVCE) Methods
UVCEs are among the most serious scenarios in QRA consequence assessments, due to the potential huge and large impact on people and assets. The main model and summary of each model are presented as below.
Equivalent TNT Mass Method
- Compare heat of combustion with the energy release of TNT which is equivalent to 4.69×106 J/kg

Multi-Energy Model (MEM)
- Blast pressure is determined by charts which is defined by scaled pressure and scaled duration against a scaled distance;
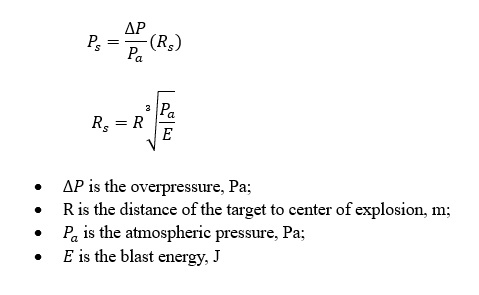
Baker Strehlow Tang (BST)
- BST methodology requires selection of the maximum flame speed, on the basis of the combined effects of congestion, fuel reactivity, and confinement.
- Congestion levels for BST is segregated by area blockage ratio per plane, number of obstacle layers, and pitch.
- Reactivity of fuels are defined by burning velocity (Su);
- Then, the flame speed correlations are determined by congestion and reactivity.
- Blast pressure is defined by above factor including the applying of the chart scaled pressure and scaled duration against a scaled distance same as MEM method.